Почему никто не понимает, насколько быстро будет развиваться искусственный интеллект?
ИИ совершенствуется во многих областях науки и отраслях промышленности. Но можно ли узнать насколько быстро совершенствуется искусственный интеллект.
Сейчас многие из нас знакомы с законом Мура, знаменитым принципом, согласно которому развитие вычислительной мощности следует по экспоненциальной кривой, удваивая в соотношении цена-качество (то есть, в скорости за единицу стоимости) каждые 18 месяцев или около того. Когда дело доходит до применения закона Мура к их собственным бизнес-стратегиям, даже дальновидные мыслители не видят огромного «слепого пятна ИИ».
Как развивается искусственный интеллект
Даже самые успешные, стратегически мыслящие деловые люди, которые видят свою отрасль насквозь, не в силах понять, что такое экспоненциальное развитие. И на этой экспоненциальной кривой есть одна технология, которая особенно извлекает выгоду из экспоненты: искусственный интеллект.
Экспоненциальные кривые на бумаге
Одна из причин, по которой люди не понимают, насколько быстро развивается искусственный интеллект, простая до смешного: экспоненциальные кривые не очень хорошо смотрятся, когда мы, люди, пытаемся объяснить их на бумаге.
По практическим соображениям практически невозможно полностью изобразить крутую траекторию экспоненциальной кривой на небольшом пространстве, таком как диаграмма или слайд.
Визуально изобразить ранние этапы экспоненциальной кривой несложно. Но поскольку более крутая ее часть стремительно наращивает обороты, все становится сложнее.
Чтобы решить эту проблему неадекватного визуального пространства, мы используем удобный математический трюк — логарифм. Благодаря «логарифмической шкале», мы научились скручивать экспоненциальные кривые.
К сожалению, широкое использование логарифмических шкал также может вызывать научную близорукость.
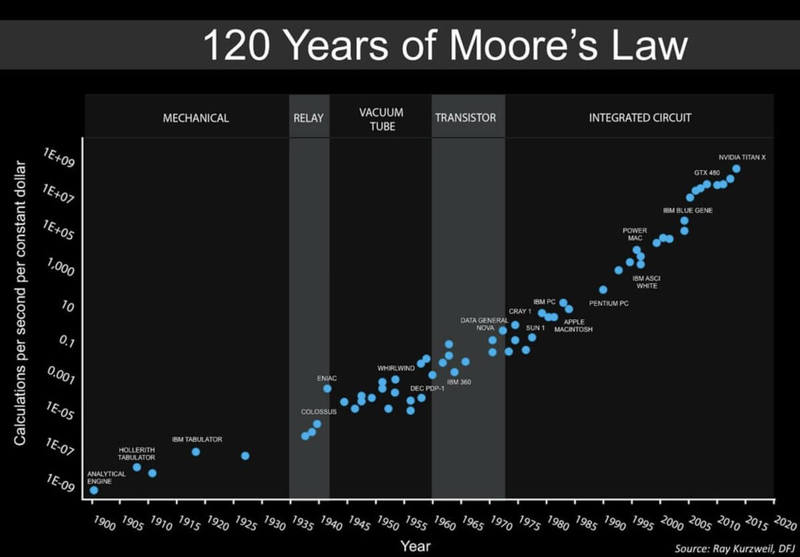
Диаграмма 1
Логарифмическая шкала устроена так, что каждый тик на вертикальной оси yсоответствует не постоянному увеличению (как в обычном линейном масштабе), а кратному, например, 100.
Классическая диаграмма закона Мура (диаграмма 1) использует логарифмическую шкалу для экспоненциального улучшения стоимости вычислительной мощности (измеряемой в вычислениях/в секунду/на доллар) за последние 120 лет, от механических устройств 1900-х до современных видеокарт на базе кремния.
Логарифмические диаграммы стали ценной формой сокращения для людей, которые осознают визуальное искажение, которое присутствуют на таких диаграммах. Сейчас это удобный и компактный способ отобразить любую кривую, которая быстро и радикально растет с течением времени.
Однако логарифмические диаграммы обманывают человеческий глаз.
Математически сжимая огромные числа, логарифмы заставляют экспоненциальный рост выглядеть линейным. Поскольку они сжимают экспоненты до линейных графиков, людям удобнее на них смотреть и рассуждать о грядущей прибавке в вычислительной мощности.
Наши логические мозги понимают логарифмические линейки. Но наши подсознательные мозги видят кривые линии и настраиваются на них.
Что же делать? Во-первых, нужно вернуться к первоначальной линейной шкале.
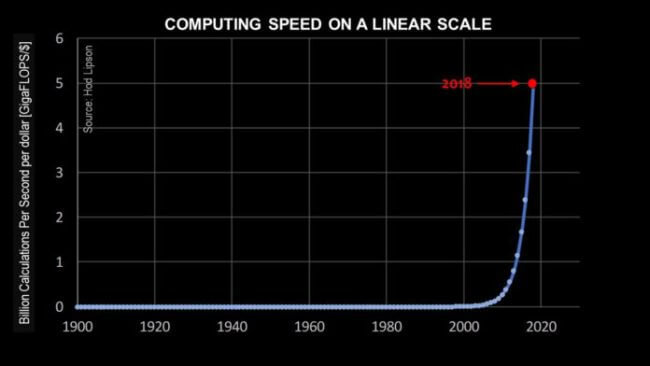
На второй диаграмме ниже данные соответствуют экспоненциальной кривой, однако вписаны в линейный масштаб по вертикальной оси. Опять же, вертикальная шкала представляет вычислительную скорость (в гигафлопах), которую можно купить за один доллар, а горизонтальная ось представляет время.
Однако на диаграмме 2 каждый тик на вертикальной оси соответствует простому линейному увеличению только одного гигафлопа (а не увеличения в 100 раз, как на диаграмме 1. Флоп — стандартный способ измерения скорости вычислений, что означает «операции с плавающей запятой в секунду».
Диаграмма 2
Диаграмма 2 показывает фактическую, настоящую экспоненциальную кривую, которая характеризует закон Мура. Глядя на то, как нарисована эта диаграмма, нашим человеческим глазам легко понять, как быстро выросла производительность компьютеров за последние десять лет.
Но со второй диаграммой что-то не так. Может показаться, что за 20 век стоимость и производительность компьютеров вообще не улучшались. Очевидно, это не так.
Диаграмма 2 показывает, что использование линейной шкалы для демонстрации изменения закона Мура со временем может ослеплять. Прошлое кажется плоским, как будто никакого прогресса не было. Кроме того, люди ошибочно заключают, что текущая точка во времени представляет период уникального, «почти вертикального» технологического прогресса.
Линейные шкалы могут обманывать людей, заставляя их верить, что они живут на вершине перемен.
Слепое пятно живущего в настоящем
Давайте еще раз взглянем на диаграмму 2. Если смотреть из 2018 года, предыдущие удвоения цены-качества, которые происходили каждое десятилетие на протяжении большей части 20 века, кажутся плоскими, почти несущественными. Человек, изучающий эту диаграмму, сказал бы: как же мне повезло жить сейчас. Я помню год 2009, когда я думал, что мой новый айфон быстрый. Я и понятия не имел, насколько он медленный. Хорошо, что я достиг вертикальной части.
Люди говорят, что мы прошли «излом хоккейной клюшки». Но такой точки перехода нет.
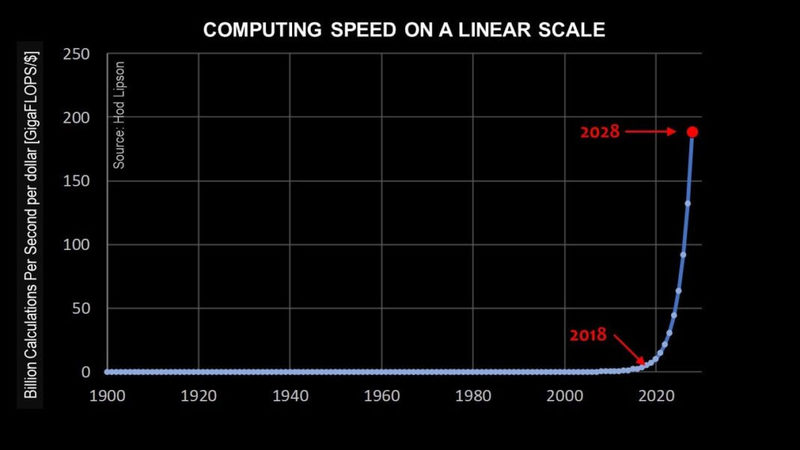
Любая форма кривой в будущем выглядит так же, как выглядела в прошлом. Ниже, диаграмма 3 показывает экспоненциальную кривую закона Мура в линейном масштабе, но на этот раз с точки зрения 2028 года.
Кривая предполагает, что рост, который мы пережили за последние 100 лет, продолжится еще как минимум 10 лет. Эта диаграмма показывает, что в 2028 году за один доллар можно будет купить 200 гигафлоп вычислительной мощности.
Диаграмма 3
Но при этом диаграмма 3 также представляет ловушку для аналитика.
Посмотрите внимательно, где именно современная вычислительная мощность (2018 год) лежит на кривой, изображенной на третьей диаграмме. С точки зрения человека, живущего и работающего в будущем 2028 году, казалось бы, в течение начала 20 века улучшений в вычислительной мощности практически не было.
Похоже, что вычислительные устройства, используемые в 2018 году были чуть мощнее тех, что использовались в 1950 году. Наблюдатель также мог бы заключить, что нынешний 2028 год представляет собой кульминацию закона Мура, где прогресс вычислительной мощности, наконец, взлетает до небес.
Каждый год можно было бы воссоздавать диаграмму 3, меняя только изображенный промежуток времени. Форма кривой была бы идентичной, менялись бы только тики по вертикальной шкале.
Обратите внимание, что форма диаграмм 2 и 3 выглядит одинаково, за исключением вертикальной шкалы. На каждом таком графике каждый прошлый момент был бы плоским, если смотреть с будущего, и каждый будущий момент был бы резким отходом от прошлого.
Увы, такое ошибочное восприятие было бы следствием ошибочной бизнес-стратегии, по крайней мере если речь касается искусственного интеллекта.
Что это значит?
Экспоненциальные темы изменений трудно понять человеческому разуму и увидеть глазом. Экспоненциальные кривые уникальны в том смысле, что они математически самоподобны в каждой точке.
Это означает, что всегда удваивающаяся кривая не имеет плоских частей, не имеет восходящих частей, изгибов и изломов, о которых говорят люди. Ее форма будет одинаковой всегда.
Поскольку закон Мура продолжает работать, возникает соблазн считать, что именно в этот самый момент мы достигли уникального этапа великих изменений в развитии искусственного интеллекта (или любой другой технологии, которая распространяется на закон Мура).
Однако, до тех пор, пока вычислительная мощность продолжает следовать экспоненциальной кривой цены-качества, каждое будущее поколение, скорее всего, будет оглядываться на прошлое как на эпоху относительно небольшого прогресса.
В свою очередь, останется верным и обратное: каждое текущее поколение будет смотреть на 10 лет в будущее и не сможем оценить, как много прогресса в области ИИ еще впереди.
Таким образом, для любого, кто планирует будущее, движимое экспоненциальным ростом вычислений, рождается задача побороть собственные ошибочные интерпретации. Нужно иметь в виду сразу три диаграммы, чтобы по-настоящему оценить силу экспоненциального роста. Потому что прошлое всегда будет выглядеть ровным, а будущее всегда будет выглядеть вертикально. опубликовано econet.ru
Если у вас возникли вопросы по этой теме, задайте их специалистам и читателям нашего проекта здесь.
P.S. И помните, всего лишь изменяя свое потребление - мы вместе изменяем мир! © econet
Источник: https://econet.ru./
Понравилась статья? Напишите свое мнение в комментариях.


Добавить комментарий